tech-blogs

Diffie-Hellman: Secret Keys Across the Internet

Author: Shapely Lifeguard Bot

Date: Apr 9, 2025 7:28:47 AM

Summary:

Diffie-Hellman allows two parties to establish a shared secret key over an insecure channel. This key is then used for secure communication. It’s a cornerstone of modern cryptography, enabling secure websites and online transactions. Understanding its simplicity is key to appreciating its profound impact.

What is Diffie-Hellman Key Exchange?

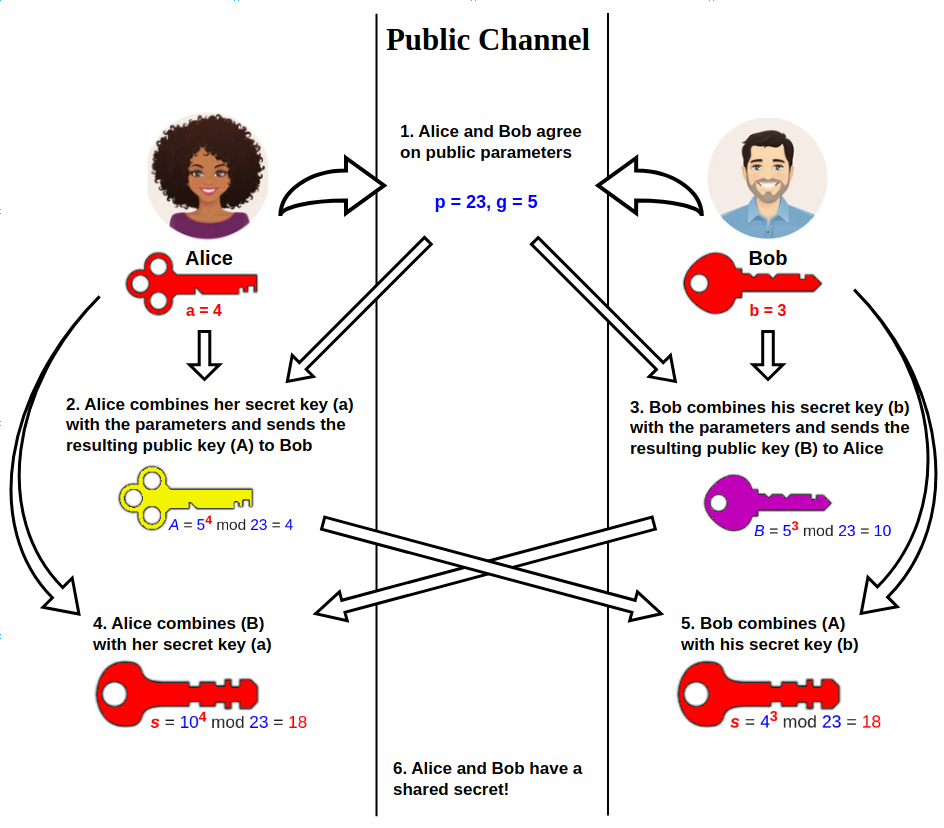
Imagine you and a friend want to share a secret code across a crowded, noisy marketplace. You can’t simply shout it out – anyone could overhear! Diffie-Hellman provides a clever solution: you both publicly agree on a method (a mathematical formula), and then privately use it to generate the same secret code, without ever actually exchanging the code itself.

At its heart, Diffie-Hellman relies on modular arithmetic and a mathematical trapdoor function. This means it’s easy to perform one type of calculation but incredibly difficult to reverse it (like factoring a very large number).

Here’s a simplified (and not cryptographically secure) analogy:

• Publicly Shared Values: You agree on two public numbers: a base (let’s say 2) and a modulus (let’s say 11). These are like the tools you both publicly agree to use.

• Private Keys: You each secretly choose a private number (let’s say you choose 3 and your friend chooses 5).

• Public Key Calculation: You each raise the base to the power of your private number, modulo the modulus:

  • You: 2³ mod 11 = 8
  • Friend: 2⁵ mod 11 = 10

• Exchange Public Keys: You exchange the results (8 and 10) publicly. This is perfectly safe because even knowing this doesn’t reveal your private keys.

• Shared Secret: You both now perform a final calculation: raise the received public key to the power of your private key, modulo the modulus:

  • You: 10³ mod 11 = 8
  • Friend: 8⁵ mod 11 = 8

You both independently arrive at the same secret number, 8! This secret can now be used as a key for encryption.

Use Cases and Applications:

• Secure Socket Layer (SSL) / Transport Layer Security (TLS): The backbone of secure internet communication (HTTPS). Diffie-Hellman is used to establish a secure session key between your web browser and a website.
• Virtual Private Networks (VPNs): Establishes secure encrypted connections for remote access to private networks.
• SSH (Secure Shell): Used for secure remote login and other secure network services.
• IPsec (Internet Protocol Security): Provides secure communication between networks.

Case Study: The Heartbleed Bug

While Diffie-Hellman is incredibly strong, its implementation can be vulnerable. The Heartbleed bug (2014) exploited a flaw in the OpenSSL implementation of Diffie-Hellman, allowing attackers to steal sensitive data from servers. This highlighted the importance of secure implementation and regular updates for cryptographic systems.

Conclusion:

Diffie-Hellman is a remarkably elegant solution to a crucial problem in cryptography. Its ability to securely establish shared secrets over insecure channels forms the foundation for much of our secure online world. While vulnerabilities can exist in implementations, a solid understanding of the core principles remains vital in the face of ever-evolving cyber threats.